Ce chapitre fait suite à celui sur le produit scalaire qui nous permet de déterminer l'équation cartésienne d'une droite à partir d'un vecteur. On verra aussi l'équation cartésienne du cercle et le projeté orthogonal d'un point.
Pour rappel, le produit scalaire possède deux définitions équivalentes, la géométrique et l'analytique : $$\vec{u}.\vec{v} = ||\vec{u}|| ||\vec{v}|| cos(\hat{(\vec{u}; \vec{v})})$$
$$\vec{u}.\vec{v} = ||\vec{u}|| ||\vec{v}|| cos(\hat{(\vec{u}; \vec{v})})$$
 $$ \vec{u}.\vec{v} = xx' + yy'$$
$$ \vec{u}.\vec{v} = xx' + yy'$$
 Ou dit plus simplement, ce pont permet de faire de la géométrie sans l'observation, mais seulement par le calcul. C'est grâce à ça qu'il est possible de modéliser numériquement notre environnement ou de faire de la géométrie dans des dimensions supérieures à 2...
Ou dit plus simplement, ce pont permet de faire de la géométrie sans l'observation, mais seulement par le calcul. C'est grâce à ça qu'il est possible de modéliser numériquement notre environnement ou de faire de la géométrie dans des dimensions supérieures à 2...
 Mais ce n'est pas si nouveau car nous avons déjà fait de la géométrie analytique par le passé avec les formules de la distance et celle du milieu de deux points...
Mais ce n'est pas si nouveau car nous avons déjà fait de la géométrie analytique par le passé avec les formules de la distance et celle du milieu de deux points...
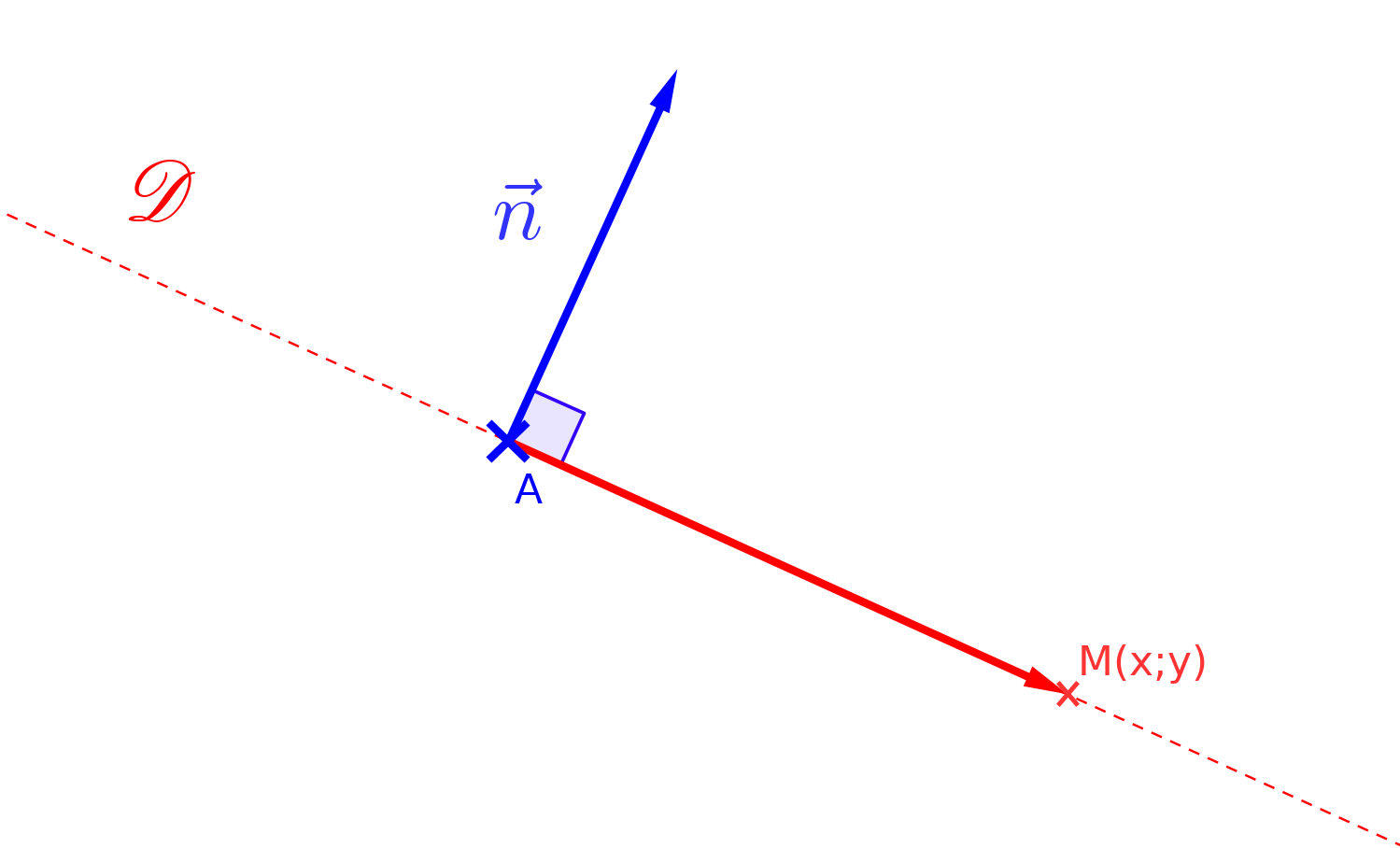 On dit que $\overrightarrow{n}$ est un vecteur normal à $\mathscr{D}$
On dit que $\overrightarrow{n}$ est un vecteur normal à $\mathscr{D}$
Le vecteur $\vec{n}$ n'est pas horizontal (vecteur normal non vectical) donc la droite coupe l'axe des abscisses en un point $A(x_A; 0)$. On applique à ses coordonnées l'équation cartésienne : $$ \begin{array}{lll} 3\times x_A - 0 + 1 &=& 0 \\ 3\times x_A &=& -1 \\ x_A &=& \frac{-1}{3} \end{array} $$ La droite passe donc par le point $A(\frac{-1}{3};0)$
De plus comme $A \in (d)$ ses coordonnées vérifient l'équation de $(d)$ et donc : $$-2\times 1+3\times 2 +c=0 \Leftrightarrow c=-4$$ Ainsi $(d)$ admet comme équation $-2x+3y-4=0$
Une application consiste à calculer le point d'intersection entre deux droites. Plus concrètement, imaginez qu'une des droite représente un écran et l'autre un rayon de lumière. Ca devient un problème d'optique.
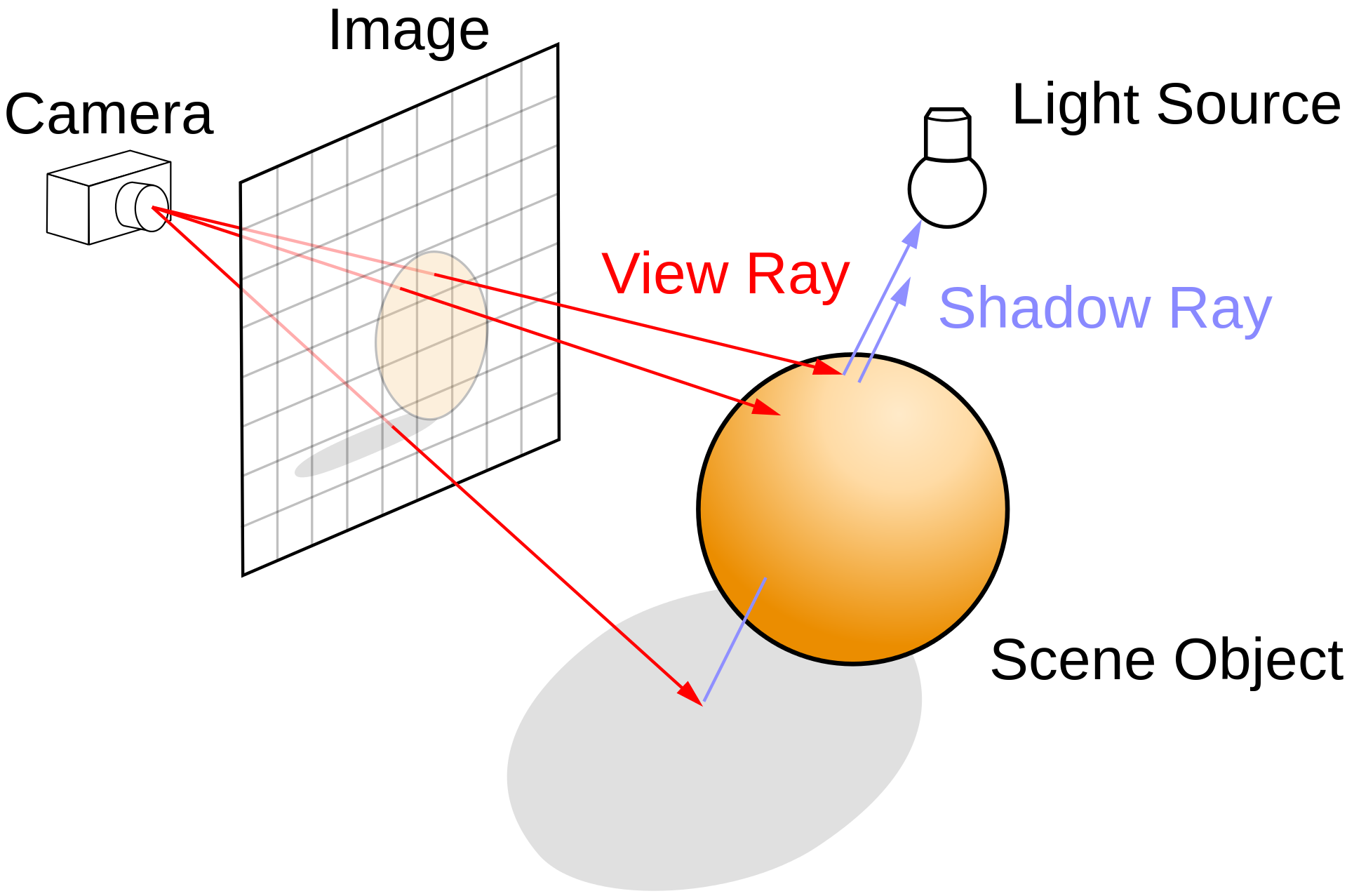 En 3D, ce calcul est à la base d'une technique de synthèse d'images numériques : le "ray-tracing". Pour la culture et pour ceux qui seraient intéressés par l'évolution du gaming, cette vidéo tente d'expliquer cette notion :
En 3D, ce calcul est à la base d'une technique de synthèse d'images numériques : le "ray-tracing". Pour la culture et pour ceux qui seraient intéressés par l'évolution du gaming, cette vidéo tente d'expliquer cette notion :
Vous pouvez découvrir la méthode et vous entraîner avec cet exerciseur :
Exercices généré automatiquement : intersections entre deux droites
Commençons par enfoncer une porte ouverte : un point $M$ est sur un cercle de centre $\Omega$ et de rayon $R$ si le segment $[\Omega M]$ est un rayon, c'est à dire, si la distance $\Omega M = R$.
On peut en déduire une condition simple sur les coordonnés de $M(x;y)$ sous la forme d'une équation. Ci-dessous, vous pouvez modifier le rayon $R$ et le centre $\Omega$ :
- Si on reconnaît la formule $(x-x_{\Omega})^2+(y-y_{\Omega})^2=R^2$, on peut directement lire les coordonnées du centre et le rayon.
- Sinon, en utilisant la technique de "semi-factorisation" utilisée pour obtenir la forme canonique d'un polynôme du second degré on peut arriver à mettre en évidence une équation sous la forme précédente et ainsi y lire les coordonnées du centre et la valeur du rayon
Il reste ensuite à exprimer le produit scalaire en fonction des coordonnées.
projections orthogonales
(perspective)
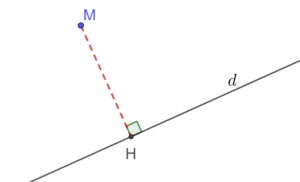
Exercices généré automatiquement : calculer les coordonnées du projeté orthogonal d'un point sur une droite
