- En premier lieu, nous présenterons dans ce document l'interface web réalisée. Un menu principal permet de choisir le niveau de difficulté d'une partie de sudoku jouable à la souris, au clavier ou en tactile. L'apparence s'adapte à l'écran utilisé ou à la taille de la fenêtre dynamiquement.
- Nous présenterons ensuite comment les parties ont été générées en programmation Python au préalable. On détaillera les classes crées pour représenter les grilles, les parties de sudoku, et les données utiles pour le jeu web. Nous présenterons plus en détail l'algorithme de résolution qui sert à la fois à générer les solutions, les grilles partielles, et à évaluer la difficulté d'une partie.
- Nous présenterons enfin des développement possibles pour des séquences pédagogiques pour la filière NSI en lien avec le programme.
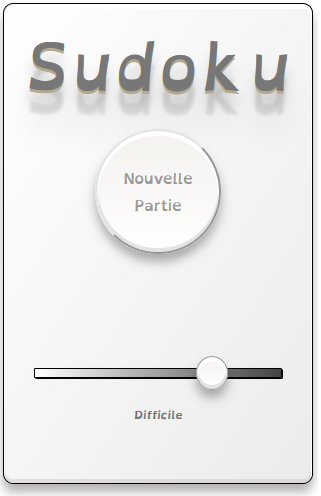
Au démarrage, le menu principal est affiché. Celui-ci comprend le titre, un bouton pour lancer le jeu, un élément de choix de la difficulté actualisant le commentaire (facile, moyen, ...), et un élément pour revenir à la partie en cours (non visible au début).
Après avoir sélectionné et cliqué sur la difficulté, le menu principal est masqué, une grille est tirée au hasard (parmi environ une centaine selon la difficulté souhaitée) et la zone de jeu est affichée.
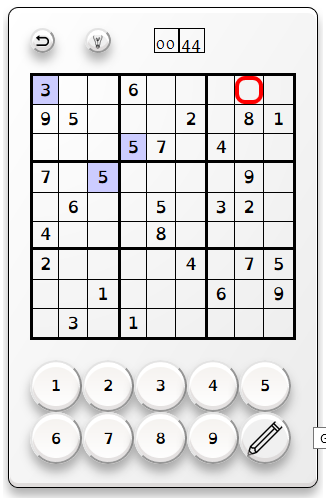
Il est possible de jouer au clavier avec les flèches de direction et le pavé numérique ou à la souris/tactile en utilisant les boutons de l'interface. Les boutons chiffres permettent de proposer un numéro à la case sélectionnée qui sera ajouté (en bleu) si il est compatible selon les règles du sudoku (même si il ne correspond pas à la solution). Si le numéro proposé n'est pas compatible, une animation sobre indiquera les incompatibilités.
Le bouton "crayon" quand il est activé permet de noter des candidats supposés. Les erreurs ne sont pas indiquées en mode crayon.
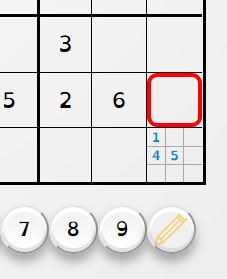
Un bouton "indice" permet de révéler la case sélectionnée. Il n'y a pas de limitation au nombre d'indices utilisé, mais la case révélée gardera une coloration jaune.
Le menu comprend également une horloge et un bouton de retour au menu qui permet de mettre le jeu en pause afin d'y revenir plus tard.
Lorsqu'une ligne ou un carré est complété, une animation récompense le joueur. De même lorsque la partie est gagnée.
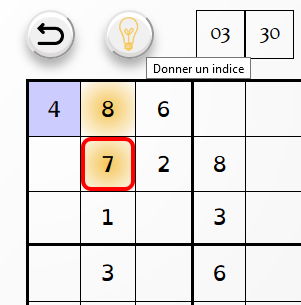
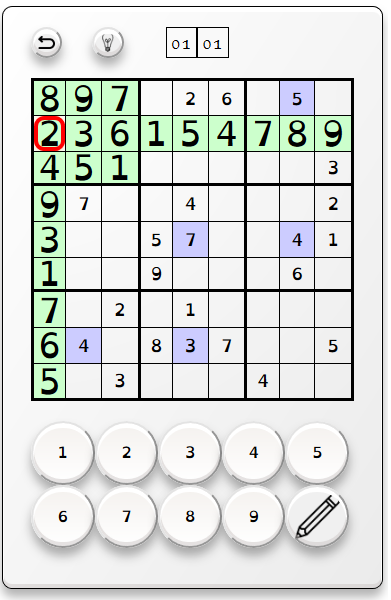
L'interface web est composée de trois fichiers sudoku.html, sudoku.css, sudoku.js et un dossier ressources contenant trois sous-dossiers images, fonts et sudoku_files.
<div class="theater-sudoku"> qui contient le menu principal <div class="menu-main-sudoku"> et la zone de jeu <div class="partie-sudoku">. Le menu principal comprend le titre <h1>, un bouton <button class="new-game-sudoku"> pour lancer le jeu, un élément de choix de la difficulté <input type="range">, et un autre bouton pour revenir à la partie en cours (non visible au début). La zone de jeu est vide au départ, et sera complétée par manipulation du DOM en JavaScript.
Sudoku() représentant l'état formel d'une partie de Sudoku tout en gérant le rendu graphique par manipulation du DOM (sans manipulation directe de la CSS). Par exemple, en modifiant dynamiquement la classe ou un attribut d'un élément du DOM représentant une case, la CSS reconnaîtra ses états et modifiera couleur, visibilité ou taille des caractères.
<div class="theater-sudoku"> au démarrage et lorsque la fenêtre est redimensionnée.
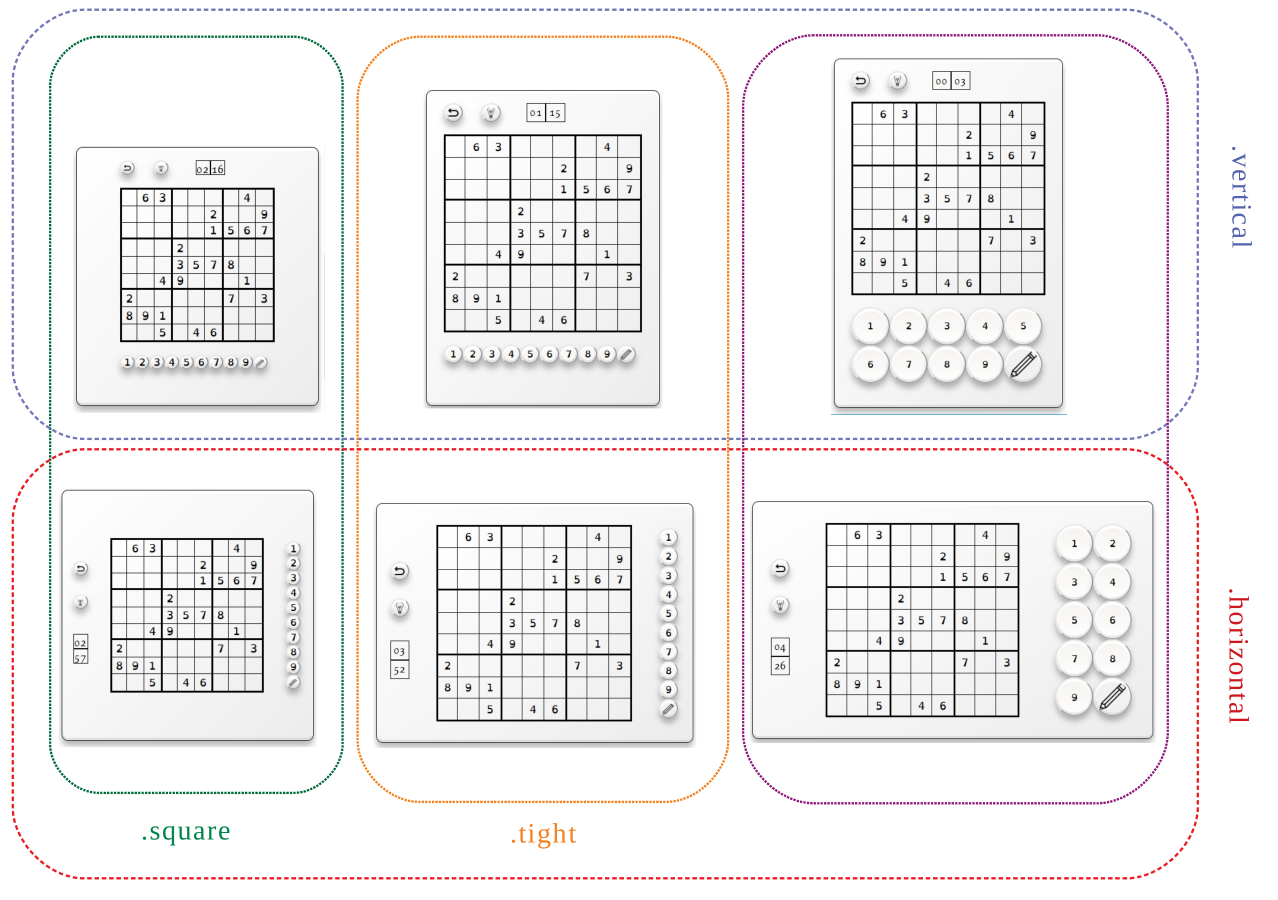La grille de sudoku étant carrée, des solutions ont été imaginées à partir de différents écrans pour laisser la place aux deux barres de menu. Selon les cas, quatre classes (.horizontal, .vertical, .tight, .square) peuvent être combinées et rendre six interfaces différentes (voir figure ci-avant). En notant H la hauteur et L la largeur, on résume ces classes par le tableau suivant :
| Classe | Condition | Commentaire |
|---|---|---|
| .horizontal | H < L | les menus sont latéraux à la grille. Par défaut les boutons sont gros pour être adaptés aux smartphones. |
| .vertical | L < H | les menus sont au dessus et en dessous de la grille. Gros boutons. |
| .tight | L / 1.5 < H < 1.5×L | la taille des boutons est plus réduite. Adapté aux navigateurs desktop. |
| .square | 0.9 × L < H < 1.3×L | les dimensions sont trop "carrées" pour laisser la place au menu. On réduit la taille de la grille de 40% |
Sudoku.handleResize() :
@media (min-aspect-ratio: 2/3) and (max-aspect-ratio: 3/2) {...}.
Ce type de condition ne s'applique qu'à un media (écran, imprimante, braille, synthèse vocale, ...). Nous souhaitions faire porter les conditions sur l'élément <div class="theater-sudoku"> et avons donc écarté cette solution pourtant plus élégante.
- La grille solution comporte les 81 nombres entiers entre 1 et 9
- La grille partielle est compatible avec la grille solution et comporte des 0 pour représenter les trous
- Les deux listes de backtrack contiennent les indices des cases sur lesquelles est revenu le programme python pour générer la grille. Elles ne servent pas à l'interface et ne sont utilisées que pour la partie python.
- trous donne le nombre de 0 dans la grille partielle et n'est pas non plus utilisé dans cette partie.
Nous n'utilisons pas la syntaxe des classes JavaScript, mais celle basée sur les prototypes.
L'objet Sudoku est structuré de la manière suivante :init() sont les suivants :
| Attribut | Commentaire |
|---|---|
container |
Objet du DOM qui contiendra la zone de jeu <div class="partie-sudoku" > |
grille_partielle |
Liste de 81 nombres entiers entre 0 et 9 qui représente l'état initial. Il provient de l'attribut de l'objet json présenté avant. |
grille_solution |
Liste de 81 nombres entiers entre 1 et 9 qui représente la solution. Il provient de l'attribut de l'objet json présenté avant. |
grille_joueur |
Cette troisième grille représente l'état courant de la partie et est initialisé par une copie de grille_partielle |
selectedCase |
Un entier entre -1 et 80 qui correspond à l'indice de la case sélectionnée par le joueur dans l'interface (-1 pour aucune case sélectionnée) |
Sudoku.lastId |
Variable de classe comptabilisant le nombre de parties courantes dans le document. |
timeout |
Référence de la prochaine animation. null signifie aucune animation |
init() sont les suivantes :
| Méthode | Commentaire |
|---|---|
setMenuNav() |
méthode graphique : crée le menu de navigation |
setSudokuElement() |
méthode graphique : crée la grille à partir de la grille partielle et du conteneur |
setMenuInputs() |
méthode graphique : crée le menu de jeu |
setSplashYouWin() |
méthode graphique : crée le contexte nécessaire à l'animation de victoire (invisible au départ) |
setEvenements() |
initialise les évènements clavier/souris |
handleResize() |
Redimensionne l'interface graphique selon la taille et la forme de l'écran (voir la partie responsive design) |
setClock() |
crée et lance l'horloge |
.sudoku. Sont contenu est généré par la fonction initSudokuFromMenu(). Elle contient 81 éléments de classe .case dont les bordures (en css) dessinent la grille. Chacune des case contient un élément de classe .num dont le contenu HTML est la valeur dans la case si il y en a une. Afin de présenter sa structure, nous prenons l'exemple suivant :
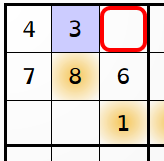Le code HTML qui lui correspond est le suivant :
.num dans chaque élément .case répond à la nécessité de centrer verticalement les chiffres de la grille. Nous avons choisit d'attribuer la valeur flex à l'attribut CSS display des élément num. Cette solution fonctionnait indépendamment de la hauteur des conteneurs et de la taille de la font utilisée.
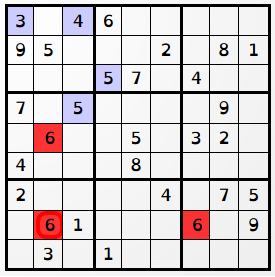
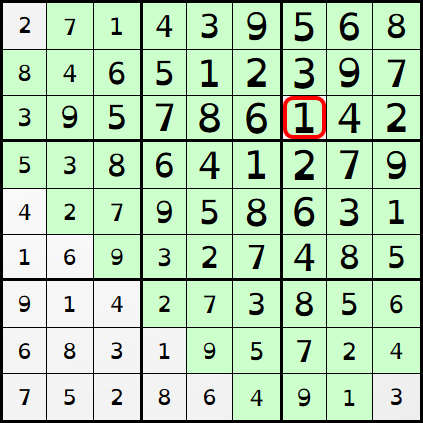
grilleur_joueur de l'objet JS Sudoku. Le style conditionné par les attributs des éléments HTML .case et .num permet de visualiser les valeurs d'origine (fond blanc), les valeurs trouvées (fond bleu), les valeurs données en indice (fond jaune), la case sélectionnée (bord rouge) et les animations en vert.
| Attribut | Commentaire |
|---|---|
value |
Renseigne sur l'origine de la valeur présente :
|
index |
indice de la case dans la grille (entre 0 et 80). Permet au script d'identifier une case avec une requête comme :
document.querySelector('#sudoku0 .num[index='12']")
|
selected |
seule valeur possible true. Indique la case sélectionnée. |
L'élément num peut également contenir un élément de classe nums-crayon contenant lui-même 9 éléments representant les valeurs possible de "mode crayon".
Les chiffres proposés par le joueur sont ajoutés via la méthode Sudoku.addNum() qui effectue les actions suivantes :
- Vérifier si une animation est en cours (auquel cas elle n'effectue pas l'action)
- Vérifie si le mode "crayon" est activé. Une case déjà remplie refusera d'être éditée en mode crayon.
- Vérifie la compatibilité du nombre proposé dans la grille
- Lance une animation pour indiquer le succés ou l'échec de la tentative
Sudoku.addNum() ne fait que modifier les attributs des éléments HTML décrits avant. Les animations et les styles sont décrits en CSS.
addEventListener(eventType, f) de l'objet EventTarget permet d'appeler une fonction f à chaque fois qu'un évènement de type eventType ("click", "scroll", "load", etc.) est détecté. N'importe quel objet du DOM peut être une cible (y compris document et window)
<div class="theater-sudoku"> et ses fils sont nécessaire pour initialiser le sudoku. C'est que réalise la dernière instruction du script dans le fichier sudoku.js :
initMenuSudoku() gère le choix de la difficulté (nécessitant une intervention de JavaScript pour le sous-texte), rend le menu visible, masque la zone de jeu et définit les évènements liés aux boutons <button class=".new-game-sudoku"> et <button class=".back"> en utilisant addEventListener(eventType, f) :
-
La fonction
showSudoku()masque le menu et affiche le conteneur de la zone de jeu. -
La fonction
initSudokuFromMenu()charge un fichier json de manière asynchrone et génère la grille graphique à partir de lui.
Sudoku.setEvenements() initialise la détection des évènements nécessaires au jeu. this fait référence à l'instance de Sudoku() :
| Méthode | Commentaire |
|---|---|
caseClick() |
Lorsqu'une case est cliquée, elle l'attribut HTML selected prend la valeur true, la case précédente est désélectionnée, et l'indice de la case est affecté à l'attribut this.selectCase.
|
buttonClick(e) |
Détecte le bouton du menu cliqué (chiffres ou indice) et appelle la méthode Sudoku.addNum(num, valueType) qui modifiera la grille selon le modèle détaillé dans la partie 2.c. Dans la fonction, e.target designe l'objet HTML button cliqué. |
caseKey(e) |
Détecte la touche de clavier pressée en ne tenant compte que des chiffres, des touches i (pour indice), c (pour crayon) et des flèches de direction. Dans la fonction, e.key est une chaîne de caractère désignant la touche pressée. e.preventDefault() permet désactiver le scrolling provoqué par les touhces haut et bas. La méthode Sudoku.addNum(num, valueType) est utilisée pour les chiffres et Sudoku.moveCase(direction) pour déplacer la case sélectionnée. |
handleResize() |
La méthode handleResize() est déjà décrite dans la partie 1.c |
showMenu() |
Affiche le menu et masque la zone de jeu. La fonction showSudoku() réalise l'opération inverse. |
toggleCrayon() |
Active/désactive le mode crayon en modifiant la classe de l'élément HTML. Cette fonction mime le fonctionnement d'une checkbox qu'il aurait été plus simple d'utiliser. Pour des raisons de "charte graphique cohérente" et d'économie de code, nous avons préféré utiliser un bouton. |
Ces animations sont décrites de la manière suivante :
incompatible des cases concernées prennent la valeur true. Cela permet à la CSS d'appliquer les animation num_incompatible et shake pendant une seconde :
incompatible au delà de cette durée afin d'éviter des incohérences dans la grille plus tard. Nous avons ajouté une méthode Sudoku.setAttributeFor=function(el, attr, val, t, f) qui sera utile pour toutes les animations :
-
el: élément HTML concerné -
attr: nom de l'attribut à ajouter -
val: valeur que doit prendre cet attribut -
t: durée avant de retirer l'attribut -
f: fonction à exécuter à la fin de cette durée (nulle par défaut)
Cela est réalisé par la méthode Sudoku.animWin(casesIndex) qui s'applique à une liste de cases, et se rappelle récursivement au bout de 20ms sur les voisins, jusqu'à épuisement à l'aide de la fonction setTimeout(fonction, durée) :
.clock). Les secondes sont des éléments .s et les minutes .m. Elle sont combinées avec les classes des unités .u et des dizaines d. On précise la durée entre deux animations :
.clock .s .u{animation-delay:attr(num)s;}. On doit donc préciser son délai pour chaque valeur :
animation-play-state pour lui donner les valeurs paused ou running.
loadJsonFile tire au hasard un nombre entre 0 et les nombre maximal de fichiers contenu dans le dossier de la difficulté sélectionnée. Une requête est envoyée à l'adresse du fichier, et lorsqu'une réponse est renvoyée, l'object JSON est parsé puis une fonction de callback l'utilise pour générer la grille :
element.querySelector(selecteur_css) ou element.querySelectorAll(selecteur_css) sont emplement suffisantes. Nous raccourcissons la syntaxe de la manière suivante :
| Attribut | Commentaire |
|---|---|
ordre_aleatoire
|
une liste mélangée aléatoirement des 81 premiers entiers. Elle permet de parcourir aléatoirement les valeurs de la grille lorsque c'est nécessaire. |
valeurs_possibles
|
liste de 81 listes. Chaque liste correspond à des candidats possibles pour la case correspondant au même indice. Ces valeurs seront mélangées aléatoirement. |
| Méthodes | Commentaire |
|---|---|
reset_grille()
|
initialise la grille à 81 valeurs nulles. |
set_valeur_possible(i, valeurs)
|
permet d'indiquer les valeurs à tester pour une case vide. Si aucune valeur n'est donnée, les entiers de 1 à 9 dans le désordre sont ajoutés. |
clone()
|
renvoie une copie de la grille. Nécessaire pour la génération de grilles partielles. |
coord_case(index)
|
Renvoie les coordonnées matricielles correspondantes à l'indice index.
|
get_val(*args)
|
Renvoie la valeur de la case. Un ou plusieurs arguments permettent d'utiliser la méthode en coordonnées matricielles ou non. |
count(num)
|
Renvoie le nombre d'éléments num dans la grille. Utile pour compter le nombre de trous.
|
count_in_row(num, index_row), count_in_col(num, index_col), count_in_square(num, index_square)
|
Renvoie le nombre d'éléments num dans la ligne, la colonne ou le carré indiqué. Utilisé pour testé la compatibilité d'une valeur
|
compatible(index_case, num)
|
teste la compatibilité d'une valeur dans une case suivant les règles du sudoku |
retirer(n_valeurs)
|
retire le nombre de valeurs indiquées suivant l'ordre de l'attribut ordre_aleatoire. Utilisé pour générer des grilles partielles à partir d'une solution (voir partie III.2.D)
|
retirer_min_contraintes()
|
retire une case dont les contraintes sur la grille sont minimales. Utile pour générer des grilles difficiles partielles difficiles à partir d'une solution (voir partie III.2.E) |
| Attributs | Commentaire |
|---|---|
grille_solution |
initialement vide, contiendra un objet Grille complet et correct selon les règles du sudoku après l'appel de la méthode genere_grille_solution()
|
grille_partielle |
initialement vide, contiendra un objet Grillepartiel, compatible avec grille_solution après l'appel de la méthode genere_grille_partielle()
|
| Méthodes | Commentaire |
|---|---|
solver(n_solution_max) |
méthode centrale : renvoie au plus n_solutions_max solutions compatibles avec grille_partielle. Voir le détail en partie III.2.B
|
genere_grille_solution() |
génère une grille solution à partir de la méthode solver(1) et l'affecte à l'attribut grille_solution
|
genere_grille_partielle(methode) |
génère une grille partielle à partir de la grille_solution selon deux méthodes possibles (détaillée plus loin) et l'affecte à grille_partielle
|
JSON |
retourne une valeur de type string représentant une version JSON de l'objet Sudoku concerné. |
saveJSON(path) |
Sauvegarde dans un fichier JSON la valeur retournée par la méthode JSON()
|
loadJSON(path) |
Permet d'instancier l'objet à partir d'attributs sauvegardés sous forme d'un fichier JSON |
JSON(), saveJSON() et loadJSON() permettront de conserver les grille déjà générées, de le réutiliser sans temps de calcul, de les incorporer à l'application web facilement et de réaliser des statistiques afin d'évaluer la difficulté.
- On considère la case sur la laquelle on se trouve
- On teste ses candidats jusqu'à en trouver un compatible (on les retire au fur et à mesure) :
- Si un candidat est compatible, on l'ajoute à la grille et on avance jusqu'à la prochaine case libre
- Si les candidats sont épuisés on les réinitialise puis on recule jusqu'à la dernière case remplie
- Appliqué à une grille vide, le solver génèrera une grille solution pleine.
- Appliqué à une grille partielle, le solver génèrera une solution si il en existe, ou reculera jusqu'à la "case -1" sinon
Nmax. Celà nous permettra plus loin de tester l'unicité d'une solution :
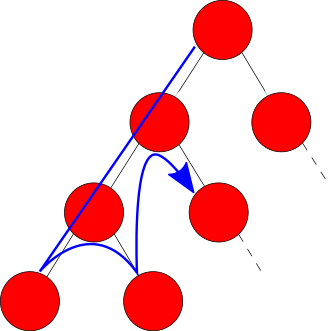
grille_solution prend les valeurs successives de ces noeuds. L'espace des solutions $\mathcal{S}$ est strictement inclu dans $\mathcal{E}=\{0,1,...,9\}^{81}$. Le parcours exhaustif de $\mathcal{E}$ est assuré par la partie suivante de l'algorithme :
-
Tant Que longueur(solutions) < NmaxDans notre contexte,
Nmaxvaut 1 ou 2. On ne parcourt donc $\mathcal{E}$ entièrement que dans le cas où il n'y a pas de solution (ce n'est jamais le cas), ou si la première solution rencontrée est à la fin de l'ordre de parcours de l'arbre (ce qui n'est vraisemblablement pas le cas et hors du cadre d'étude du projet). On ne s'intéresse donc qu'à un sous-ensemble très réduit de $\mathcal{S}$ -
grille_solution = grille_partielleLorsque nous recherchons une solution à partir d'une grille partielle (avec garantie d'existence d'une solution), nous excluons de fait un nombre important de grilles.
-
Si val compatible avec grille_solutionNous excluons les grilles incompatibles avec les règles du sudoku. Pour chaque noeud incompatible de l'arbre, l'ensemble de ses descendants est ignoré car aucun n'appartient à l'espace des solutions $\mathcal{S}$
De plus, cette condition garantie qu'à chaque étape
grille_solutionreprésente une grille de sudoku (éventuellement partielle) compatible avec les conditions initiales.
Nmax).
- Générer une grille solution complète de 81 cases
- Retirer une case tant que la solution est unique
- Retenir l'avant dernière grille partielle
Solver permet de résoudre les deux problèmes :
- appliqué à une grille vide avec Nmax = 1 en paramètre, il construit une grille solution.
-
appliqué à une grille partielle avec Nmax = 2, il permet de tester l'unicité de la solution :
- la grille partielle possède une solution par construction, donc l'algo renverra au moins une solution
- si l'algo renvoie deux solution, la grille est "dégénérée" car ne possède pas de solution unique
- sinon une solution est unique, on peut continuer à retirer des valeurs
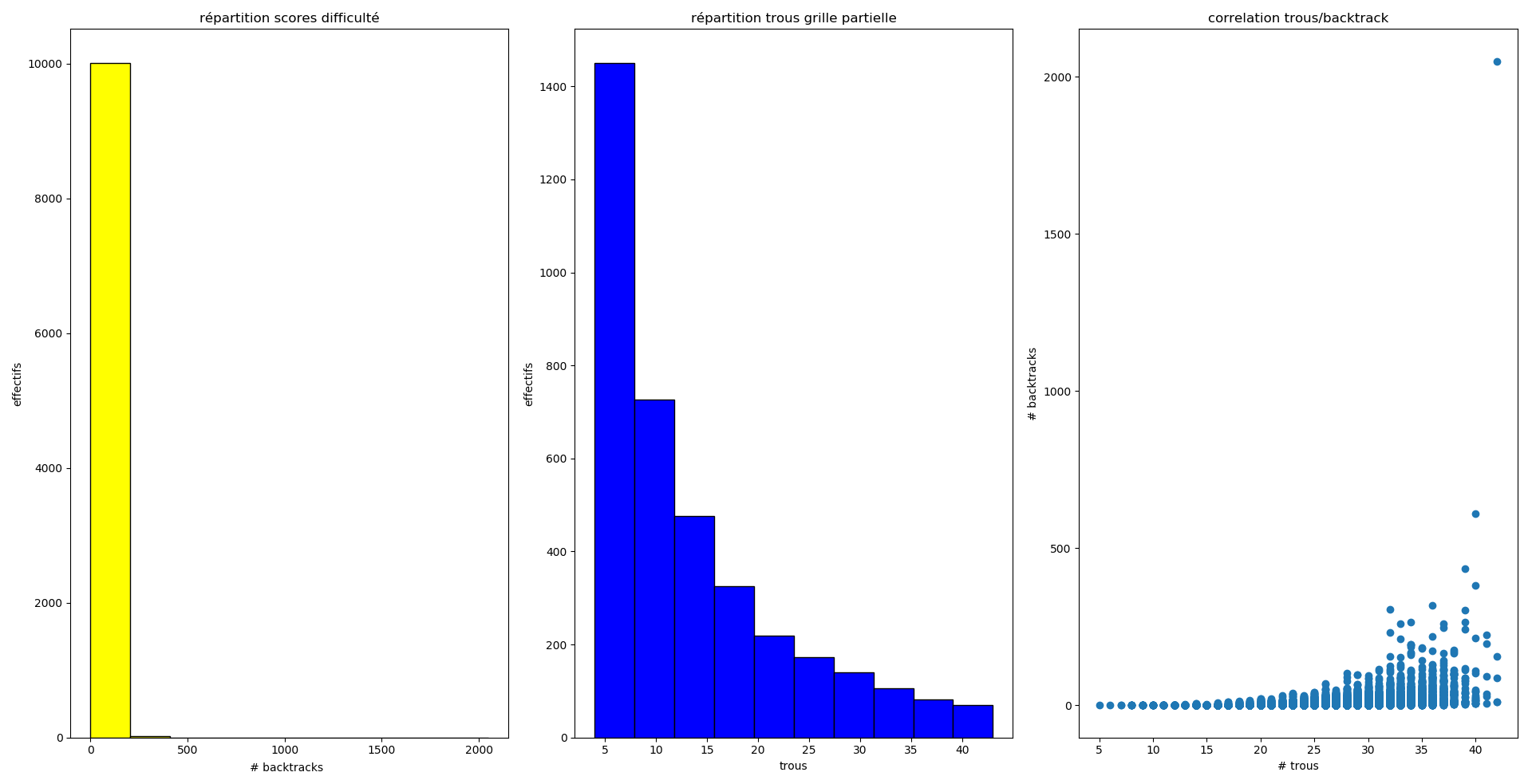
- le nombre de trous, compris entre 5 et 42, admet une moyenne de 26,15.
- le nombre de retours arrières utilisés par le solver pour résoudre la grille partielle, compris entre 0 et 2049 admet une valeur moyenne de 8,75.
- Dans 95% des cas, ce nombre de retours est inférieur à 36.
On se place dans le contexte d'une grille partielle. Soit $C$ une case remplie contenant une valeur $k\in\{1,...9\}$. Nous appelons degré de contrainte de $C$ , le nombre de cases vides de la grille pour lesquelles $k$ serait un candidat, si la case $C$ était vidée.
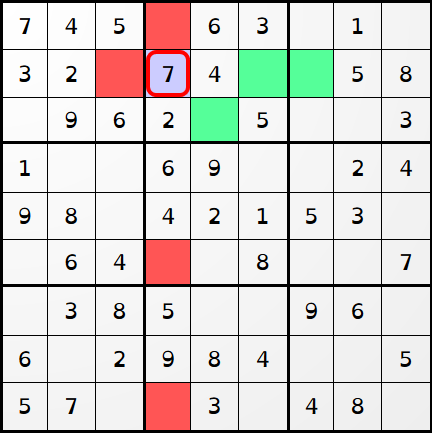La case sélectionnée impose donc 3 contraintes sur la grille.
A chaque étape, il faut évaluer les contraintes de chaque case de la grille partielle par la méthode Grille.evalContraintesGrille(). On retire alors une case de degré de contrainte minimal. L'algorithme général reste le même, seul l'ordre de choix des cases diffère.
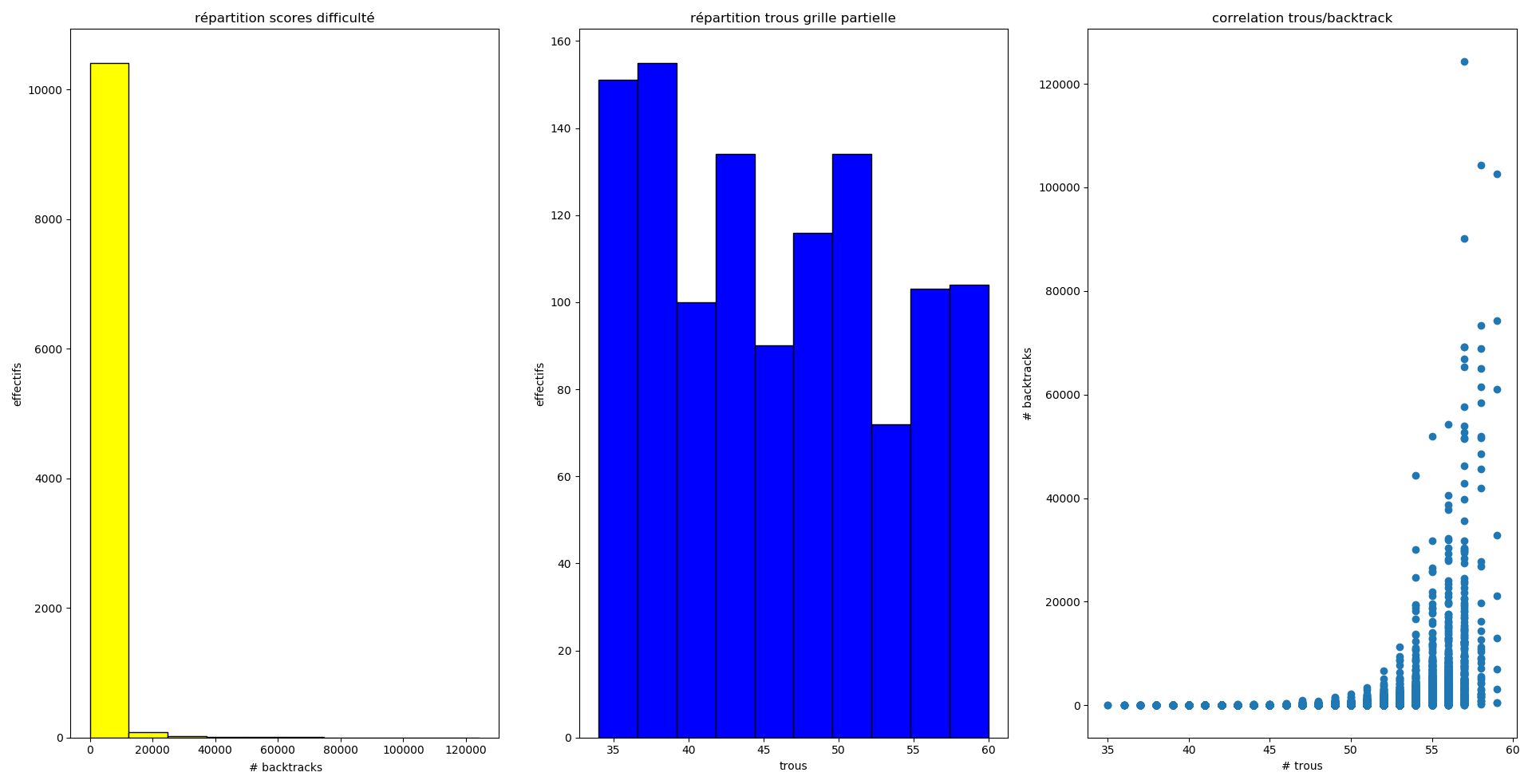
- le nombre de trous, compris entre 35 et 59, admet une moyenne de 49,5.
- le nombre de retours arrières utilisés par le solver pour résoudre la grille partielle, compris entre 0 et 124364, admet une valeur moyenne de 936,7.
- Dans 95% des cas, ce nombre de retours est inférieur à 3656.
La difficulté des grilles a été évaluée empiriquement à l'aide du jugement d'une (bonne) joueuse de sudoku, et en comparant les grille à une application mobile populaire. Nous souhaitions proposer 5 niveaux de difficulté : débutant, facile, moyen, difficile et expert. Les critères objectifs dont nous disposions étaient le nombre de trous et le nombre de backtracks nécessaires pour résoudre automatiquement la grille. C'est en ajustant ces paramètres que nous obtenons les conditions de difficulté suivantes :
- Débutant : $backtracks \lt 5000$ et $ 30 \lt trous \lt 40$
- Facile : $backtracks \lt 5000$ et $ 45 \lt trous \lt 50$
- Moyen : $5000 \lt backtracks \lt 10000$ et $ 45 \lt trous \lt 50$
- Difficile : $5000 \lt backtracks \lt 10000$ et $ 50 \lt trous \lt 57$
- Expert : $backtracks \gt 20000$ et $ trous \gt 57$
Afin de générer un grand nombre de parties, la fonction genere_sudoku_jsons(n, methode) est utilisée. n est un entier désignant le nombre de parties souhaitées, methode une chaîne de caractères indiquant l'une des deux méthodes souhaitées. La fonction ajoute les parties sous forme de fichiers JSON dans un sous-dossier (un pour chaque méthode), trace des histogrammes en utilisant la librairie matplotlib et indique quelques données statistiques en utilisant la librairie numpy.
DataSudoku a été créée. Les attributs principaux sont :
| Attribut | Commentaire |
|---|---|
dir |
Le chemin vers le dossier contenant les parties json à traiter. Attribut obligatoire pour instancier un objet DataSudoku |
files |
La liste des fichiers contenus dans le répertoire dir
|
sudokus |
La liste des objets de classe Sudoku chargés à partir des fichiers json
|
selection |
Une sous-liste de sudokus de sudokus peuplée par la méthode select
|
| Méthode | Commentaire |
|---|---|
select(condition)
|
parcourt la liste sudokus et ajoute à selection ceux qui satisfont la condition. L'argument condition est une fonction qui prend en argument un objet de classe Sudoku et renvoie un booléen |
copyToDir(dirPath) |
Convertit les parties de selection en fichier json et les copie dans le répertoire désigné par dirPath. Permet de récupérer les parties selon des conditions de difficulté.
|
histogrammes |
Trace des histogrammes des partie de sudokus visualisant le nombre de trous et le nombre de backtracks. Affiche via la console des informations statistiques (min, max, moyenne, médianne, quartiles)
|
- Création d'une grille en html avec mise en forme CSS
- Création dynamique d'une grille à partir d'une liste en JavaScript en axant sur les boucles
- Utilisation des animations CSS pour programmer une horloge numérique, puis analogique.
- Interface clavier-souris et boutons avec gestion des évènements afin de compléter une grille
- Création d'un menu avec choix de difficulté. Utilisation et traitement d'un formulaire
- Vérification de la compatibilité d'une valeur dans une grille selon les règles du sudoku
-
Réaliser certaines fonctions utiles :
- compter le nombre de valeurs dans une colonne/ligne/carré
- convertir indices de cases en coordonnées matricielles
- calculer l'indice du carré d'une case
- tester la compatibilité d'une valeur dans une case
- sélectionner les cases incompatibles en cas d'erreur
- Décrire un algorithme de résolution du sudoku (backtracking) en séance débranchée.
- Décrire un algorithme de création d'une grille partielle à partir d'une grille solution. Essayer de faire émerger la notion d'unicité, et l'importance de l'existence d'une solution.
- Idée de preuve de correction de l'algorithme.
- Dénombrement des parties possibles